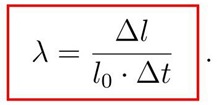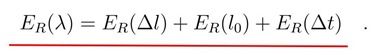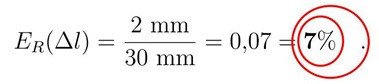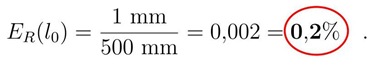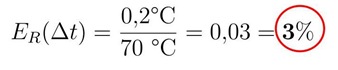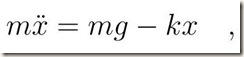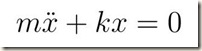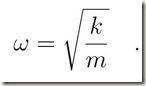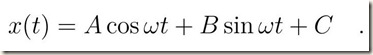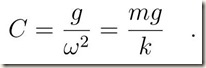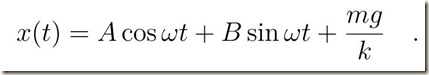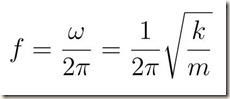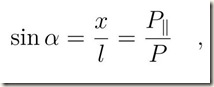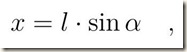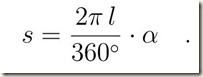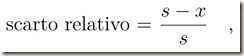Condizione di equilibrio.
Consideriamo un corpo vincolato in un suo punto
O al quale siano applicate due forze.
La condizione necessaria affinché il corpo rimanga in equilibrio è che il momento risultante delle forze applicate al corpo, calcolato rispetto al punto O di vincolo, sia nullo.
Ricordiamo che il
momento di una forza rispetto ad un punto è il prodotto dell’intensità della forza per la distanza tra la forza (cioè la retta su cui essa giace) ed il punto in questione.
Possiamo constatare la validità della condizione di equilibrio anche semplicemente esaminando la foto qui sotto.
Indichiamo con 1 le grandezze fisiche relative ai pesi a sinistra e con 2 quelle relative a i pesi a destra del perno centrale O.
Dato che la sbarra è in equilibrio sotto l’azione dei pesi applicati, deve valere la condizione:
ora, poiché abbiamo
la condizione di equilibrio si può scrivere così:
Tale condizione significa che si può ottenere equilibrio variando forze e distanze,
purché le intensità delle due forze siano inversamente proporzionali alle corrispondenti distanze dal punto di vincolo; in simboli:
Misura delle distanze.
Possiamo verificare la validità di questa condizione anche esaminando la fotografia.
I programmi che consentono di modificare le foto (ad es. GIMP) consentono anche di rilevare la posizione di un punto fornendone le coordinate in pixel. Potremmo quindi determinare le distanze in millimetri, semplicemente confrontandole con una distanza di riferimento, ad esempio la lunghezza dell'intera sbarra che è di 40,0 cm. Tuttavia ciò non è necessario, poiché è sufficiente confrontare tra loro le due distanze d
1 e d
2 per verificare che il loro rapporto è l'inverso del rapporto tra le forze: ovviamente, il valore del rapporto tra due distanze non dipende dall'unità di misura scelta.
Una volta note le coordinate dei punti rilevanti, le distanze tra le forze ed il punto sono semplicemente ricavabili dalle coordinate orizzontali, cioè dalle
differenze tra le ascisse dei punti interessati: questo perché le forze sono verticali per definizione, e lo sono approssimativamente anche nella foto.
Nel nostro caso le distanze tra le due forze ed il punto O risultano:
d
1 = 516 pixel ,
d
2 = 388 pixel.
Il rapporto d
2/d
1 risulta così 0,75, in ottimo accordo con il rapporto F
1/F
2 tra le forze (dato che una corrisponde a 3 pesetti e l'altra a 4 pesetti).
Incertezze nelle misure e precisione nella stima dei momenti.
Le intensità delle forze sono note con una tolleranza (dichiarata dal costruttore) inferiore all'1 %:
Le distanze sono misurate, in genere, con righe millimetrate ed hanno dunque un'incertezza relativa dell'ordine di:
La precisione consentita dagli strumenti in dotazione per la misura del momento risulta quindi: